Citation
A. Bonfanti, J.L. Kaplan, G. Charras and A. Kabla
Soft Matter 16:6002-6020 (2020)
Abstract
Abstract
Soft materials often exhibit a distinctive power-law viscoelastic response arising from broad distribution of time-scales present in their complex internal structure. A promising tool to accurately describe the rheological behaviour of soft materials is fractional calculus. However, its use in the scientific community remains limited due to the unusual notation and non-trivial properties of fractional operators. This review aims to provide a clear and accessible description of fractional viscoelastic models for a broad audience and to demonstrate the ability of these models to deliver a unified approach for the characterisation of power-law materials. The use of a consistent framework for the analysis of rheological data would help classify the empirical behaviours of soft and biological materials, and better understand their response.
Figure sample
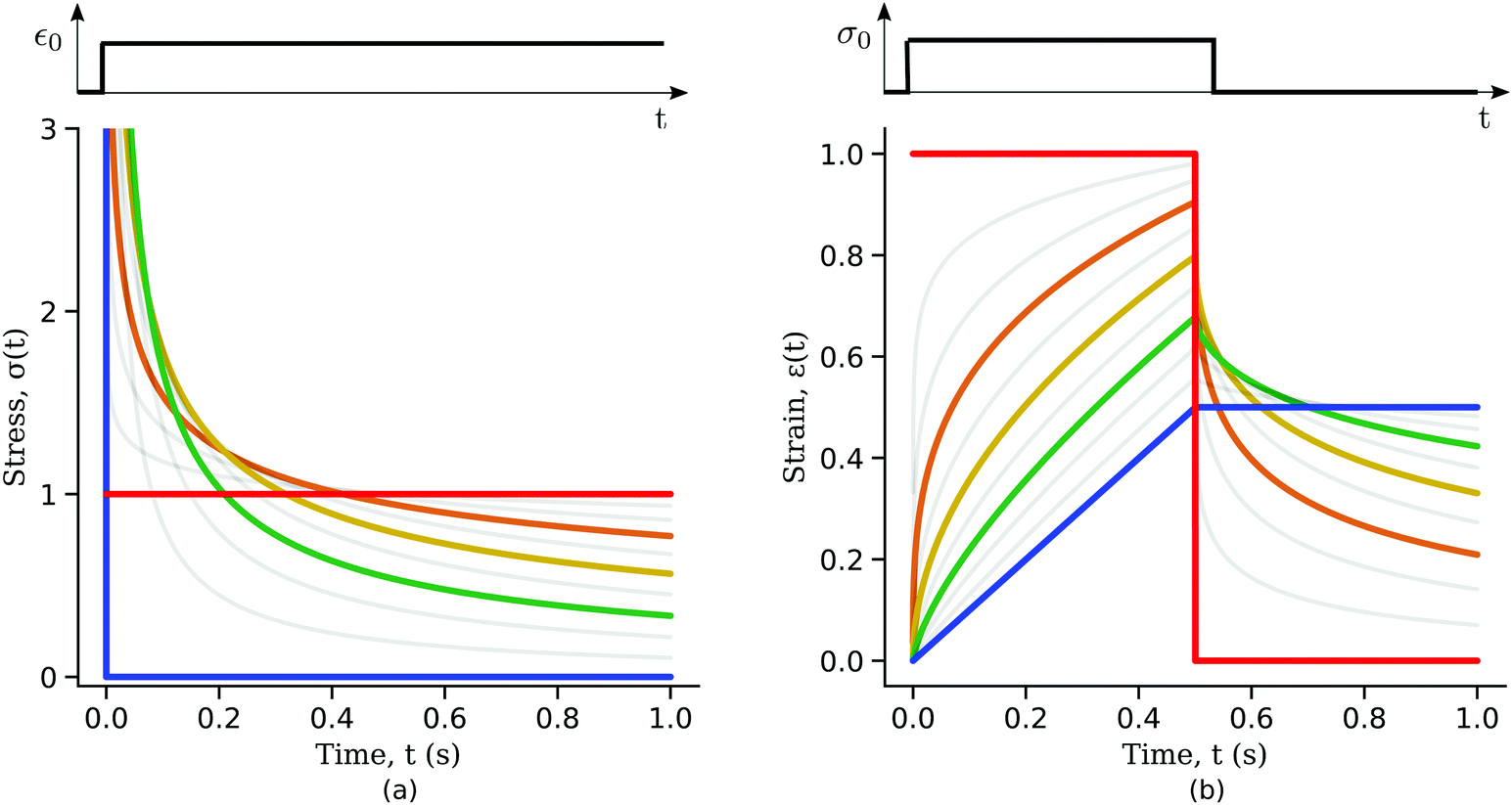
Responses of a springpot when subjected to (a) constant strain and (b) a step in stress. The red curves are the responses for a spring (β = 0), the blue curves for a dashpot (β = 1) and the grey curves are for increasing values of β from 0.1 to 0.9 (orange, yellow and green curves are respectively β = 0.3, 0.5 and 0.7).