Emergent Patterns from Probabilistic Generalisations of Lateral Activation and Inhibition

Citation

L. Willis and A. Kabla

Journal of the Royal Society Interface 13:20151077 (2016)

Abstract

The combination of laterally activating and inhibiting feedbacks is well known to spontaneously generate spatial organisation. It was introduced by Gierer and Meinhardt as an extension of Turing’s great insight, that two reacting and diffusing chemicals can spontaneously drive spatial morphogenesis per se. In this study, we develop an accessible nonlinear and discrete probabilistic model to study simple generalisations of lateral activation and inhibition. By doing so, we identify novel modes of morphogenesis beyond the familiar Turing-type modes; notably, beyond stripes, hexagonal nets, pores, and labyrinths, we identify labyrinthine highways, Kagome lattices, gyrating labyrinths, and multi-colour travelling waves and spirals. The results are discussed within the context of Turing’s original motivating interest: the mechanisms which underpin the morphogenesis of living organisms.

Figure sample

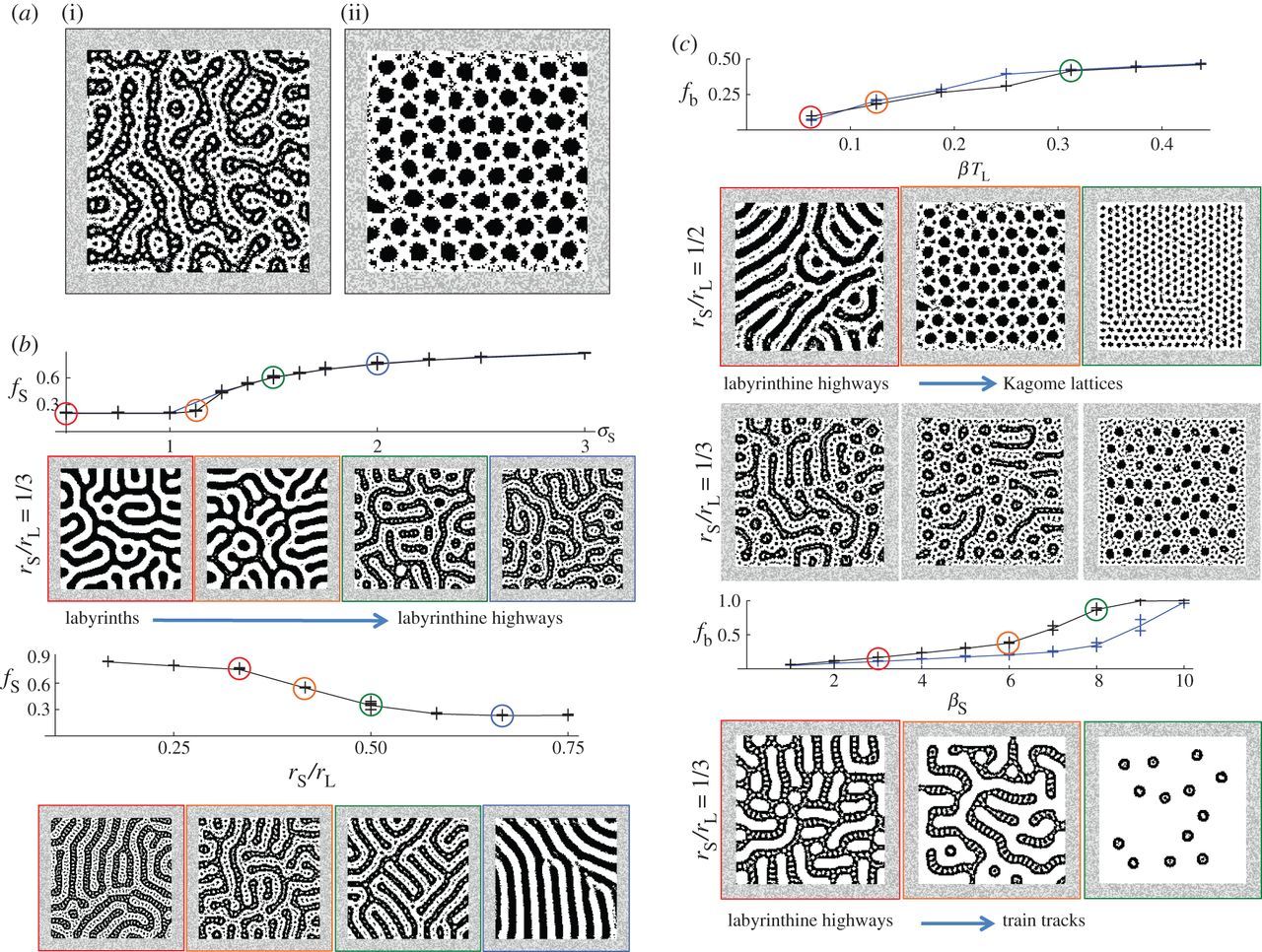
Labyrinthine highways and Kagome lattices for competing nonlinear inhibition on the short range. In all simulations, TS = TL = 1/16; other parameters are in table 1. (a) A nonlinear inhibitory lateral feedback that competes with the activatory feedback on the short range generates labyrinthine highways (i) and Kagome lattices (ii). (b) Colour symmetry. Increasing Inline Formula causes labyrinths to bifurcate to labyrinthine highways as represented by the sudden increase in fS (the black curve superposed on the blue curve is for l, rL and rS rescaled by a factor of 1.5 while other parameters are held constant). The bifurcation occurs only when rS/rL < 1/2 (lower plot). (c) Colour symmetry break. In all plots, σS = 2. Increasing β causes labyrinthine highways to bifurcate smoothly to Kagome lattices for rS/rL= 1/2 (upper blue plot) or interwoven short- and long-scale hexagonal nets for rS/rL= 1/3 (upper black plot). Increasing βS causes labyrinthine highways to bifurcate to train tracks (lower plots; blue (black) curve is for rS/rL= 1/2 (1/3)).