
Citation
A.J. Kabla, G.B. Blanchard, R.J. Adams and L. Mahadevan
Book chapter in Cell Mechanics: From Single Scale-Based Models to Multiscale Modeling, Taylor and Francis ed., pages 351-377 (2010)
Abstract
Abstract
The tissues of animal embryos utilize large-scale morphological transforma- tions to bring about highly sophisticated body plans. In contrast with plant tissues, where differential growth and change in cell shapes are the main mor- phogenetic mechanisms, animal cells have in addition the ability to move with respect to their neighboring cells. Movement can be either active (cell motility) or passive, for instance as a response to an imposed strain. Despite the progress in genetics and molecular biology, our understanding of develop- mental biology still suffers a lack of experimental description and mechanistic interpretation of how individual cell behaviors lead to well-organized collective movements at the tissue scale. One of the outstanding issues concerns the role of mechanical forces, for instance as a driving force for passive morphological changes, or as involved in signaling pathways regulating active cell behavior. In this chapter we summarize a framework specifically designed to quantify the kinematics of embryo development. By analyzing clusters of neighboring cells, we developed a multiscale geometrical description that decomposes tis- sue strains into two contributions: one associated with changes in cell shapes and the other with cell–cell slippage or motility. The emphasis on cell shapes and cell–cell slippage provides, in particular, a fully continuous framework especially suitable to capture temporal and spatial heterogeneities regardless of discrete events such as neighbor exchanges. We also show here explicitly how the statistics of cell shape changes depend on a microscopic assumption regarding cell–cell slippage and propose a simple geometrical principle that can be used to deploy a consistent and robust approach.
Figure sample
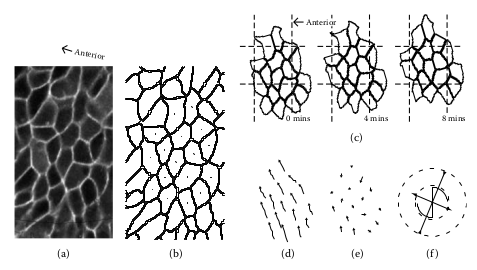
Example of tracking for a cell cohort in the zebrafish trunk. (a) Image of the first cellular layer flattened on a plane from a 3-D confocal stack. (b) Reconstructed cell membranes. (c) Evolution of a cell cohort, for the group radius corresponding to nc = 2, and δt = 8 min. (d) Displacement field calculated from the above images. (e) Residual displacements once the mean velocity is subtracted. (f) Velocity gradient tensor Lt resulting from the linearization of the velocity field. The cross indicates the direction of eigenvectors of the symmetric part Dt . The corresponding eigenvalues are coded in the length of the bars, with an arrow pointing outward for a positive eigenvalue (extension) or inward for a negative eigenvalue (convergence). The scythe motif represents the spin tensor Wt , with a diameter in proportion to the magnitude of the antisymmetrical element. The radii of the dashed circles correspond to 0.8% and 1.6% per minute.


